Subtypes¶
In some cases, Disco is willing to accept one type in place of another, when this is known to be safe. For example, suppose we have the following definitions:
f : N -> N
f(n) = sqrt(n) + 1
g : Z -> Z
g(n) = n - 5
x : N
x = 16
y : Z
y = -10
Of course we can give x as an input to f, because the type of f says
it takes natural numbers as input, and x is a natural number.
Likewise, the type of y matches g’s input type, so we can give
y as an input to g:
Disco> f(x)
5
Disco> g(y)
-15
On the other hand, we cannot give y as an input to f. f
is expecting only natural numbers as input, and it might not be safe
to give it a negative number. In fact, in this case, it’s definitely
not safe: we cannot take the square root of a negative number.
Disco> f(y)
Error: typechecking failed.
https://disco-lang.readthedocs.io/en/latest/reference/typecheck-fail.html
However, we can give x as an input to g:
Disco> g(x)
11
Why is that? Well, mathematically speaking, every natural number is
also an integer, so if a function is prepared to receive any integer
(positive or negative) as input, then giving it only natural numbers
(i.e. nonnegative integers) is perfectly safe. Intuitively, disco
automatically “converts” the natural number into an integer before
giving it to g.
Since it is always safe to use a natural number anywhere an integer is
expected, we say that N is a subtype of Z.
The four basic numeric types can be arranged in a diamond shape, like so:
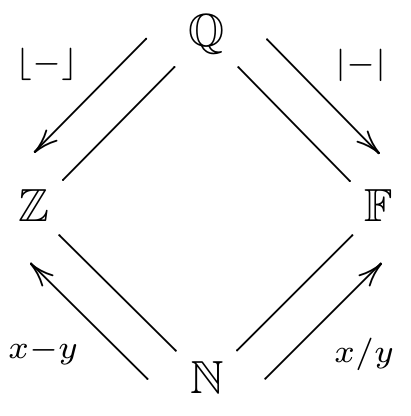
Each type is a subtype of the type or types above it. That is, Z
is a subtype of Q, F is a subtype of Q, and N is a
subtype of all the others.
Subtyping for algebraic types¶
In addition to the subtype relationships between the basic numeric types, more complex algebraic types can be subtypes of each other too.
For pair types,
A * Bis a subtype ofC * Dexactly whenAis a subtype ofC, andBis a subtype ofD. For example, given these definitions:g : Z * Q -> Q g(x,y) = y / (3x) p : N * N p = (2,5)
It is allowed to give
pas an input tog:Disco> p(g) 5/6
Since
Nis a subtype ofZ, andNis a subtype ofQ, thereforeN * Nis a subtype ofZ * Q.Similarly, for sum types,
A + Bis a subtype ofC + Dexactly whenAis a subtype ofC, andBis a subtype ofD. For example, given these definitions:g : Z + Q -> Q g(left(z)) = z / 2 g(right(y)) = 3y p : N + Z p = left(1) r : N + Z r = right(-2)
It is allowed to give
pandras inputs tog:Disco> g(p) 1/2 Disco> g(r) -6
Since
Nis a subtype ofZ, andNis a subtype ofQ, thereforeN + Nis a subtype ofZ + Q.Function types work a little differently.
A -> Bis a subtype ofC -> Dexactly whenCis a subtype ofAandBis a subtype ofD. Notice how the relationship is reversed for the input types. Working out why this makes sense is left as an interesting exercise for the reader.